个人记录&题解:
该题初学较有难度,后来看过一遍题解后自己尝试写出代码,过程中也是遇到了不少的问题。
首先该题第一步要做的一定是排序,因为题目要求不要重复的三元组,所以需要排序,接下来逐步固定住一个数字假设为a,如果找到了三元组那么a也是最小的数字,同样保证a<=b<=c这样构成的[a,b,c]三元组就是唯一的,当固定好一个后问题就简化为了从后面的数组序列中找到两数之和等于-a,然后同样逐步固定,这期间有很多需要特别注意的地方,一是不能重复,所以需要处理重复的,假设找到一个abc之后,首先b需要逐步往后递推,跳过重复的数字,找到下一个不重复的b,然后减小c,判断是否还存在b+c+a=0。
同样当b循环完一遍后,也意味着以a为第一个数字的三元组也搜索结束了,需要递推到下一个不重复数字的a开始。
代码如下:
class Solution { public List<List<Integer>> threeSum (int [] nums) { Arrays.sort(nums); int n = nums.length; List<List<Integer>> ans = new ArrayList <List<Integer>>(); for (int first = 0 ;first<n-2 ;first++){ if (first>0 && nums[first] == nums[first-1 ]) continue ; int third = n-1 ; int target = -nums[first]; for (int second = first+1 ;second<n-1 ;second++){ if (second>=third) break ; while (nums[second]+nums[third]>target&&second<third-1 ) { third--; } if (nums[second]+nums[third]<target) continue ; else if (nums[second]+nums[third]==target){ List<Integer> list=new ArrayList <Integer>(); list.add(nums[first]); list.add(nums[second]); list.add(nums[third]); ans.add(list); while (nums[second+1 ]==nums[second]&&(second<third-1 )){ second++; } if (second>=third) break ; } } } return ans; } }
思路&题解
该题很容易想到是利用滑动窗口来解决问题,但如何判断窗口内的字符串和目标字符串是否匹配是个问题。
因为是查找异位词而不是完全相等的词,因此可以考虑记录每个字母出现的次数来判断两个字符串是否互为异位词 ,后续每次移动窗口时只需要将第一个字母的count–把下一个字母的count++,再Arrays.equals()判断就可以了,代码如下:
class Solution { public List<Integer> findAnagrams (String s, String p) { int sLen = s.length(); int pLen = p.length(); if (sLen<pLen) return new ArrayList <Integer>(); int [] pCount = new int [26 ]; int [] sCount = new int [26 ]; for (int i=0 ;i<pLen;i++){ pCount[p.charAt(i)-'a' ]++; sCount[s.charAt(i)-'a' ]++; } ArrayList<Integer> result = new ArrayList <Integer>(); for (int i=0 ;i<sLen-pLen;i++){ if (Arrays.equals(pCount,sCount)){ result.add(i); } sCount[s.charAt(i)-'a' ]--; sCount[s.charAt(i+pLen)-'a' ]++; } if (Arrays.equals(pCount,sCount)){ result.add(sLen-pLen); } return result; }
子串问题
用时2h且时间复杂度很差
第一次自己做,想尝试简单的方法但是总是考虑不全情况,最后无奈使用最笨的双循环,时间复杂度很高,就算这样期间也出现了边界处理的问题,以下是我第一次自己的笨方法:
class Solution { public int subarraySum (int [] nums, int k) { int l = nums.length; if (l==0 ) return 0 ; int count = 0 ; for (int i=0 ;i<l;i++){ int temp = nums[i]; for (int j=i+1 ;j<l;j++){ if (temp==k){ count++; } temp += nums[j]; } if (temp==k)count++; } return count; } }
前缀和 :
之后看题解想到了前缀和的概念,可以先用一个数组保存原数组[0…i]的前缀和,用来快速查询数组中某一段连续序列的和,可以用来解决这道题,但仅仅用前缀和的话时间复杂度还是n方,并没有降低时间复杂度,甚至还比原来更复杂了。
超时代码如下:
class Solution { public int subarraySum (int [] nums, int k) { int count = 0 ; List<Integer> pre = new ArrayList <Integer>(); pre.add(0 ); for (int i=1 ;i<=nums.length;i++){ pre.add(nums[i-1 ]+pre.get(i-1 )); } for (int i=1 ;i<pre.size();i++){ for (int j=i;j<pre.size();j++){ if (pre.get(j)-pre.get(i-1 ) == k) count ++; } } return count++; } }
哈希表优化 如果想优化时间复杂度,可以看到可以从查找中下手,原来的每轮都需要从头查找,这里可以使用哈希表优化:
具体思路为:“哈希表的键值对分别保存某一前缀和和其出现的次数” ,这样可以导致查找符合要求的两前缀和B-A=k时可以转化为寻找是否存在某个B=k+A因为k时固定的,所以当用哈希表查找键为k+A的键时时间复杂度为O(1)。
代码如下:
class Solution { public int subarraySum (int [] nums, int k) { int count = 0 ,pre=0 ; HashMap<Integer,Integer> mp= new HashMap <Integer,Integer>(); mp.put(0 ,1 ); for (int i=0 ;i<nums.length;i++){ pre += nums[i]; if (mp.containsKey(pre-k)) { count += mp.get(pre-k); } mp.put(pre,mp.getOrDefault(pre,0 )+1 ); } return count; }
总结
哈希表在解决”两数和”类问题中的优势:
直接查找 :通过哈希表,我们可以在 O(1) 时间复杂度内查找是否存在 b = sum - a降低时间复杂度 :将暴力解法的 O(n²) 优化到 O(n)空间换时间 :牺牲 O(n) 的额外空间存储哈希表,换取时间效率的提升
应用场景总结 哈希表这种模式适用于多种变形问题:
标准两数和:找到数组中和为目标值的两个数
连续子数组和(如你之前的问题):利用前缀和+哈希表找到和为k的子数组
三数和、四数和:可以先固定一个或两个数,然后用哈希表解决剩余的”两数和”问题
差值问题:查找满足 a - b = target 的元素(等价于 a = b + target)
核心思路
遍历数组中的每个元素 a
计算需要查找的互补值 b = target - a
在哈希表中查找是否存在 b
如果存在,找到解;如果不存在,将当前元素 a 加入哈希表
继续遍历下一个元素
难度:hard 用时:6h
题目:
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
思路 :
该题目是一个滑动窗口和子串有关的问题,不看题解的之前一开始是一点思路都没有,看了题解之后的我是这样理解这道题的:
首先这道题的关键点在每次移动窗口寻找窗口内最大值时, 如果想使用保存之前最大值数字的方法,那么如果脱离了窗口大小也是不行的,所以在保存最大值的时候最好保存其在nums[]数组中的下标, 那么用什么数据机构来解决这道题呢?
这里想到的一个解法是,因为找的是最大值,所以我们每次逐步往后查找的时候只需要找更大的数字就好了,更小的不用保存,但是这样会有一个问题就是假如一个数字为7654321,k=2这样上来就是最大,后面的数字全都进不去队列中保存,因此可以考虑把数字都逐步进入队列中,但是当遇到一个更大的数字时,把队列前面比这个数小的全部移出队列,这样保存的就是一个最新最近的较大值了, 就比如例子中的数组,我们从i=0往后逐步循环nums数组,循环完三个即一个窗口时,队列中保存了一个3、-1。当-3进来的时候小于-1所以直接入队不移出任何值,但是这个时候就要注意一点是-3结束之后当前最大值3就不在窗口内了,所以需要及时判断并更新队列首(即当前最大元素)的值,将其出队。
代码如下:
class Solution { public int [] maxSlidingWindow(int [] nums, int k) { if (nums == null || nums.length == 0 ) { return new int [0 ]; } int n = nums.length; int [] result = new int [n-k+1 ]; ArrayDeque<Integer> q = new ArrayDeque <Integer>(); for (int i = 0 ; i < n; i++) { while (!q.isEmpty()&&nums[q.getLast()]<=nums[i]){ q.pollLast(); } q.addLast(i); if (i-q.getFirst()>=k) { q.pollFirst(); } if (i>=k-1 ) result[i-k+1 ] = nums[q.getFirst()]; } return result; } }
题目:
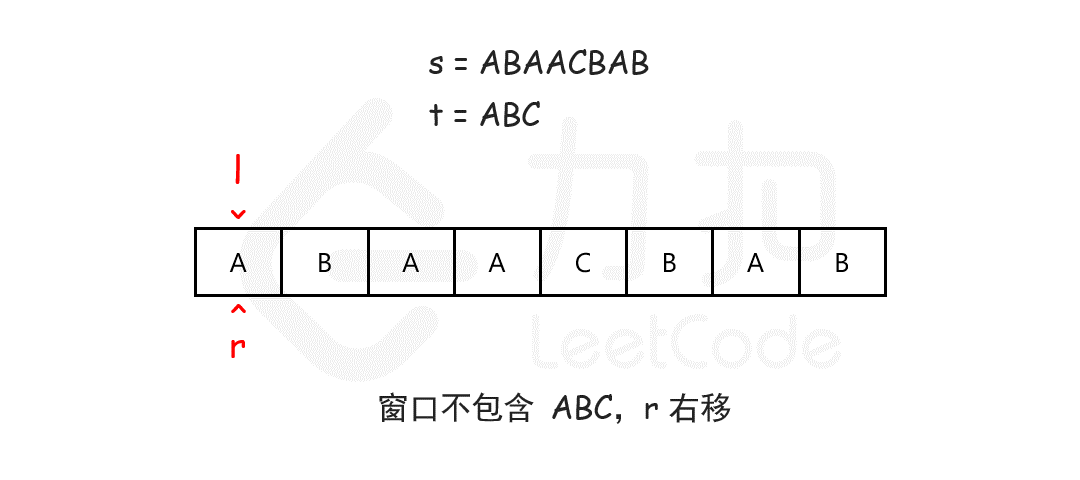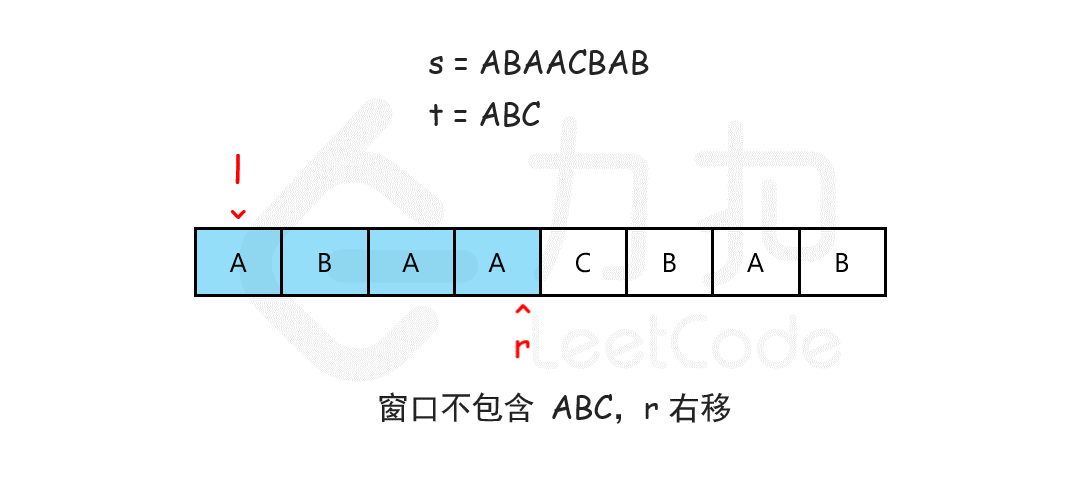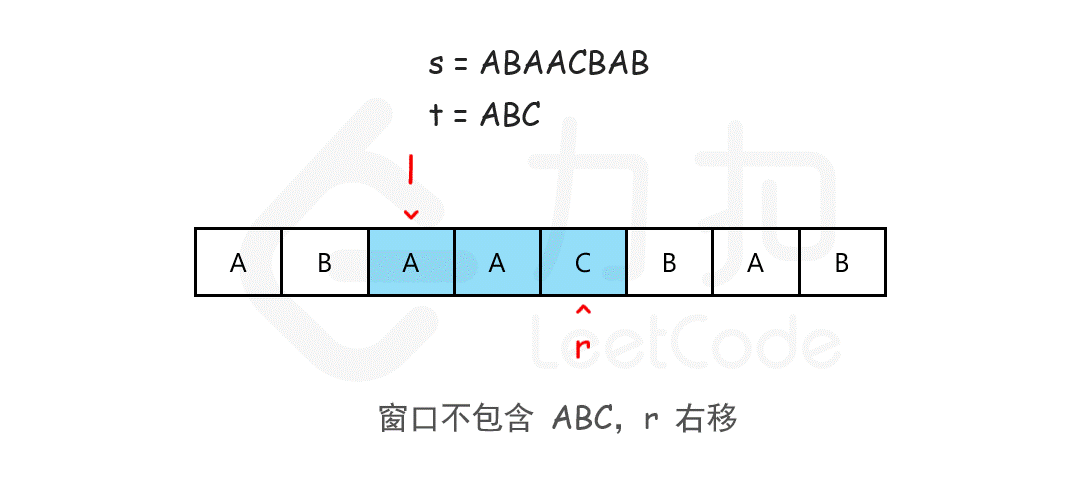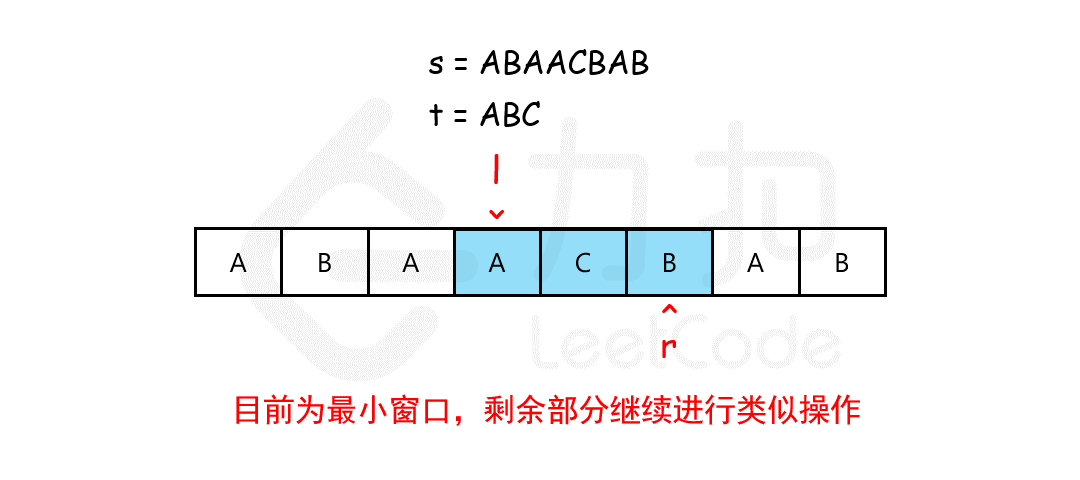
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = "ADOBECODEBANC", t = "ABC" 输出:"BANC" 解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。
困难的题目,但如果不想要优化的话其实并不是很困难。
基础解法:
使用滑动窗口思想,使用 while 收缩左边界,而不是 for 循环嵌套。设置窗口的首尾p和q,p向前逐渐找到符合的子串后缩小q找到更小的合理范围:
字符串是否符合的比较可以使用hashmap存储字符出现的次数,比较时挨个判断t字符串的每个字符是否在s中都有且次数不小于。
代码:
import java.util.*;public class Solution { public String minWindow (String s, String t) { if (s == null || t == null || s.length() < t.length()) return "" ; Map<Character, Integer> target = new HashMap <>(); Map<Character, Integer> match = new HashMap <>(); for (char c : t.toCharArray()) { target.put(c, target.getOrDefault(c, 0 ) + 1 ); } int i = 0 , j = 0 ; int min = Integer.MAX_VALUE; String ans = "" ; while (i < s.length()) { char rc = s.charAt(i); if (target.containsKey(rc)) { match.put(rc, match.getOrDefault(rc, 0 ) + 1 ); } while (ifContains(target, match)) { int curLen = i - j + 1 ; if (curLen < min) { min = curLen; ans = s.substring(j, i + 1 ); } char lc = s.charAt(j++); if (target.containsKey(lc)) { match.put(lc, match.get(lc) - 1 ); } } i++; } return ans; } private boolean ifContains (Map<Character, Integer> target, Map<Character, Integer> window) { for (Map.Entry<Character, Integer> e : target.entrySet()) { if (window.getOrDefault(e.getKey(), 0 ) < e.getValue()) { return false ; } } return true ; } }
题目:给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
学习过程:一开始就想到了前缀和或者动态规划的思想, 但感觉前缀和更简单于是就打算用前缀和算,但反复思考前缀和的递推过程给我绕昏了,以为用前缀和做不了,看到评论区发现只要很巧妙的更新前面的前缀和最小值就可以了,代码如下:
class Solution { public int maxSubArray (int [] nums) { int n = nums.length; int [] qianzhuihe = new int [n+1 ]; qianzhuihe[0 ] = 0 ; int sum = 0 ; for (int i=0 ;i<n;i++){ sum +=nums[i]; qianzhuihe[i+1 ] = sum; } int ans = Integer.MIN_VALUE; int min = 0 ; int max = 0 ; for (int i=1 ;i<n+1 ;i++){ ans = Math.max(ans,qianzhuihe[i]-min); min = Math.min(min,qianzhuihe[i]); } return ans; } }
其次还可以考虑用动态规划做,后续可以思考一下,不超过五行代码就可以搞定
题目:以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
示例 3:
输入:intervals = [[4,7],[1,4]] 输出:[[1,7]] 解释:区间 [1,4] 和 [4,7] 可被视为重叠区间。
初次思路:个人刚接触到这道题的时候,想使用纯数组求解,因此考虑设置一个很大的数组,记录下连续的区间,具体思路是初始化数组全部为0,然后把每个小区间内的值都通过判断后变为1,这样最后找连续的值只需要找连续的1就可以了,如果1中断了就说明当前的一个连续区间已经找完了,我编写了代码之后测试运行答案是对的,代码如下:
class Solution { public int [][] merge(int [][] intervals) { int [] maxArray = new int [10005 ]; int length = intervals.length; for (int i=0 ;i<length;i++){ int head = intervals[i][0 ]; int tail = intervals[i][1 ]; if (maxArray[head] == 0 && maxArray[tail] == 0 ){ for (int j=head;j<=tail;j++){ maxArray[j] = 1 ; } } else if (maxArray[head]!=0 && maxArray[tail] == 0 ){ for (int j=tail;j>head;j--){ if (maxArray[j]==1 ) break ; maxArray[j] = 1 ; } } else if (maxArray[head]==0 &&maxArray[tail]!=0 ){ for (int j=head;j<tail;j++){ if (maxArray[j]==1 ) break ; maxArray[j] = 1 ; } } } ArrayList<int []> result = new ArrayList <int []>(); for (int i=0 ;i<10005 ;i++){ if (maxArray[i] == 1 ){ int j=i; while (maxArray[j]==1 ){ j++; } result.add(new int []{i,j-1 }); i=j; } } int [][] ans = result.toArray(new int [result.size()][]); return ans; } }
但是当我提交的时候发现有一半都是错的,其中一个错误例子引起了我的注意:
输入
intervals =
[[1,4],[5,6]]
添加到测试用例
输出
[[1,6]]
预期结果
[[1,4],[5,6]]
这个例子让我恍然大悟,原来的做法是把区间看成了一个个独立的点,把连续的特征 离散化了,导致这样的例子会产生错误的结果,4-5的区间并没有被包括,但是这两个点却是连续的,在离散的看法下就导致了错误的结果。
于是我打开题解开始学习:
class Solution { public int [][] merge(int [][] intervals) { if (intervals.length == 0 ) { return new int [0 ][2 ]; } Arrays.sort(intervals, new Comparator <int []>() { public int compare (int [] interval1, int [] interval2) { return interval1[0 ] - interval2[0 ]; } }); List<int []> merged = new ArrayList <int []>(); for (int i = 0 ; i < intervals.length; ++i) { int L = intervals[i][0 ], R = intervals[i][1 ]; if (merged.size() == 0 || merged.get(merged.size() - 1 )[1 ] < L) { merged.add(new int []{L, R}); } else { merged.get(merged.size() - 1 )[1 ] = Math.max(merged.get(merged.size() - 1 )[1 ], R); } } return merged.toArray(new int [merged.size()][]); } } 作者:力扣官方题解 链接:https: 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
可以看到该题解先是对原来的区间按照左端排序后,排序后一次循环就可以统计完所有连续的区间了记为merge[],因为后面小区间的起始点要么在已经分好的merge[]中,要么就是不在,不在的话那么说明右端点更不可能合并了,可以直接将该区间加入到merge []中。